↜ Back to index Introduction to Numerical Analysis 1
Part b—Lecture 1
In the following few lectures we develop a numerical method for the heat equation, also known as the diffusion equation, modeling the evolution of temperature in a solid body or the diffusion of a chemical in a solution.
The heat equation
Let us think about a thin rod of length 1 positioned on the x-axis between 0 and 1. We suppose that the sides of the rod are kept at a constant temperature a and b, and that the temperature of the rod at time t = 0 and point x ∈ [0,1] is u_0(x). We are interested in the temperature of the rod at point x ∈ (0,1) at a later time t > 0, called u(x,t).
It is useful to think about the temperature u as a function of position x ∈ [0,1] and time t ≥ 0. Then physical Fourier’s law implies that the function u is a solution of the heat equation, a partial differential equation:
u_t(x, t) = u_{xx}(x, t), \qquad 0 < x < 1, t > 0,\\
Here u_t is the partial derivative of u with respect to t, u_t = \frac{\partial u}{\partial t} and u_{xx} is the second partial derivative u with respect to x, u_{xx} = \frac{\partial^2 u}{\partial x^2}. For u to be a solution of this equation, it needs to be once continuously differentiable in t and twice continuously differentiable in x, and the above equality be satisfied for all x \in (0, 1) and t > 0.
Example 1. Let \omega \in {\mathbb{R}} be fixed. We check that the function u(x,t) = \exp(-\omega^2 t) \sin (\omega x) is a solution of the heat equation.
We first compute the partial derivatives using the chain rule: \begin{aligned} u_t(x,t) &= -\omega^2 \exp(-\omega^2 t) \sin (\omega x),\\ u_x(x,t) &= \omega \exp(-\omega^2 t) \cos (\omega x),\\ u_{xx}(x,t) &= -\omega^2 \exp(-\omega^2 t) \sin (\omega x). \end{aligned} We see that u_t = u_{xx} everywhere and so this function is a solution of the heat equation.
Example 2. The heat equation has a very convenient property for building solutions:
- If u and v are two solutions, then u + v is also a solution.
- If u is a solution, then C u is a solution for any constant C \in {\mathbb{R}}.
Because of this, the heat equation is a linear partial differential equation.
Exercise 1. Here are a few examples of solutions of the heat equations. Check that they satisfy the heat equation for all x and t.
- u(x, t) = C for any constant C.
- u(x, t) = \exp(-\omega^2 t) \cos (\omega x) for any \omega \in {\mathbb{R}}.
- u(x, t) = \frac 1{\sqrt{t}} \exp\left(-\frac{x^2}{2t}\right)
Exercise 2. Find a \in {\mathbb{R}} so that u(x, t) = t + a x^2 + Cx is a solution for any constant C.
Enter the answer in LMS.
Since there are infinitely many solutions of the heat equation, we need to prescribe extra conditions to have a unique solutions.
We need to prescribe:
initial condition: u(x, 0) = u_0(x), the value of the temperature at the initial time t = 0. Here u_0 is a given function.
boundary condition: u(0, t) = a, u(1, t) = b, where a, b are given constants, prescribe what the temperature u is at the boundary of the domain (0, 1). This is also called the Dirichlet boundary condition.
Therefore we often write all the required conditions on the solution together:
\left\{ \begin{aligned} u_t(x, t) &= u_{xx}(x, t), && 0 < x < 1, t > 0,\\ u(x, 0) &= u_0(x), && 0 < x < 1, \\ u(0, t) &= a, && 0 < t, \\ u(1, t) &= b, && 0 < t. \end{aligned} \right.
This is called the initial value problem for the heat equation with Dirichlet boundary condition.
Example 3. Assume that a = b = 0 and u_0(x) = \sin(\pi x). Then u(x,t) = \sin(\pi x) \exp(-\pi ^2t) is the unique solution of the heat equation.
We see that the solution becomes almost 0 very fast. This is an important feature of the heat equation.
In fact, with general boundary data a, b, the solutions exponentially fast converges to the stationary solution, the function (1 - x)a + x b.
Numerical method: explicit finite difference method
In contrast to ordinary differential equations, we need to discretize derivatives both in time and in space. For the discretization of u_t, we use the same idea as for the Euler method: the Taylor series at t. Let \tau > 0 and write:
u(x, t + \tau ) = u(x, t) + \tau u_t(x, t) + O(\tau^2), where O(\tau^2) stands for higher order terms proportional to \tau^2.
We will therefore approximate
u_t(x, t) \sim \frac{u(x, t + \tau ) - u(x, t)}\tau.
For the second derivative in x, we will use a similar idea. Let h > 0 and express
\begin{aligned} u(x + h, t) &= u(x, t) + h u_x(x, t) + \frac{h^2}2 u_{xx}(x,t) + O(h^3),\\ u(x - h, t) &= u(x, t) - h u_x(x, t) + \frac{h^2}2 u_{xx}(x,t) + O(h^3). \end{aligned}
Note the opposite sign in front of the first derivative. By adding these two equalities and subtracting 2 u(x,t), we can approximate u_{xx}(x,t) as
u_{xx}(x,t) \sim \frac{u(x + h, t) - 2u(x, t) + u(x - h, t)}{h^2}.
We now select an integer M ≥ 1 and subdivide the domain (0,1) into M intervals (x_{k-1}, x_k) of length h = 1 / M for k = 1, \ldots, M. In particular, x_k = k h, k = 0, \ldots, M.
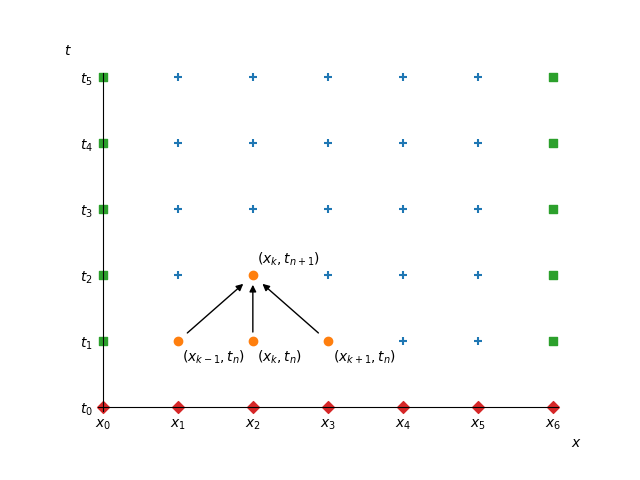
Similarly, we choose time step \tau > 0 and introduce the discrete times t_n = n \tau for n = 0, 1, \ldots. Let u_{n, k} denote the value of a numerical approximation of u(x_k, t_n). From the formulas for the approximation of u_t and u_{xx} and the heat equation, we get the forward time centered space (FTCS) numerical scheme:
\frac{u_{n+1, k} - u_{n, k}} \tau = \frac{u_{n, k - 1} - 2 u_{n, k} + u_{n, k + 1}}{h^2}, \qquad n = 0, 1, \ldots, \quad k = 1, \ldots, M-1.
The values u_{0, k} are given by the initial data u_0(x_k), and the values u_{n, 0}, u_{n, M} are given by the boundary data a and b.
We can express u_{n+1, k} in terms of u_{n, k - 1}, u_{n, k} and u_{n, k + 1}. Therefore we can advance the solution from time step n to time step n+1. This is the algorithm:
Algorithm.
Set the initial values u_{0, k} = u_0(x_k), \qquad k = 0, \ldots, M.
For every n = 0, 1, \dots, find the “new” values \left\{ \begin{aligned} u_{n+1, 0} &= a,\\ u_{n+1, k} &= u_{n, k} + \frac\tau{h^2} (u_{n, k - 1} - 2 u_{n, k} + u_{n, k + 1}), && k = 1, \ldots, M-1,\\ u_{n+1, M} &= b. \end{aligned} \right.
This algorithm is illustrated in the following figure.